Bir yağmur damlası; gök gürültüsünden geçtiğinde, rüzgardaki bir sabun köpüğü gibi damlacıkları çeken güçlü elektrik alanlarına maruz kalır. Elektrik alanı yeterince güçlüyse; damlacıkların parçalanmasına ve ince, elektrikli bir sis oluşmasına neden olabilir.
Bilim insanları; yeni kurulan elektrik hatlarına zarar veren yıldırım düşmesi endişeleriyle, 1900’lerin başlarında damlacıkların elektrik alanlarında nasıl davrandıklarını anlamaya başladılar. Yakın zamanda da; elektrik hatlarının, (kendi elektrik alanlarının) yağmur damlalarının etraflarında patlamasına neden olduğunu ve yıldırım çarpması için iletken bir yol sağladığını fark ettiler. Bu açıklama; mühendisleri yıldırım çarpmalarını sınırlandırmak için güç hatları etrafında daha kalın kaplamalar tasarlamalarına neden oldu.
Günümüzde bilim insanları, elektrik alanının ne kadar güçlü ve içinde büyük olasılıkla bir damlacık patlamasının olduğunu biliyorlar. Ancak, belirli bir damlacığın patlayacak olan tam alan kuvvetini hesaplamak; ilgili bir matematiksel bilimle açıklanabilir.
Böylece MIT araştırmacıları; bir damlacığın, elektrik alanında patladığı koşulların; ekibin ilk kez elde ettiği basit bir formüle indirildiğini buldular.
Bu basit yeni denklem ile, araştırmacılar; bir elektrik alanının damlacık patlatmak veya onu sabit tutmak için olması gereken gücü tahmin edebilirler. Formül daha önce ayrı ayrı analiz edilen üç durum için geçerlidir: Bir yüzeye sabitlenmiş, bir yüzeye kayan veya havada serbest yüzen damlacık….
Physical Review Letters dergisinde yayımlanan sonuçları; mühendislerin elektrik damlacıklarına bağlı bir dizi uygulama için elektrik alanını veya damlacıkların boyutunu ayarlamasına yardımcı olabilir. Bunlar; hava veya su arıtma, uzay ortamında itiş gücü ve moleküler analiz teknolojilerini içerir.
MIT Makine Mühendisliği ve Fizik Bölümü Lisansüstü Öğrencisi Justin Beroz: “Sonuçtan önce, mühendisler ve bilim insanları, elektrikli damlacıkların stabilitesini değerlendirmek için hesaplama açısından yoğun simülasyonlar yapmak zorunda kaldılar. Denklemimizle; basit bir kağıt-kalem hesaplamasıyla bu davranış hemen tahmin edilebilir. Bu; sıvıları ve elektriği içeren herhangi bir sistemle çalışan veya tasarlamaya çalışan mühendisler için büyük pratik yarar sağlar. ”
Damlacıklar; yüzey gerilimi, su damlacıklarının yüzeyindeki su moleküllerini bağlayan ve molekülleri içe doğru çeken yapışma kuvveti nedeniyle mükemmel küçük küreler oluşturma eğilimindedir. Damlacık; elektriksel bir alandaki kuvvet gibi başka kuvvetlerin varlığında küresel şeklinden bozulabilir. Yüzey gerilimi bir damlacığı bir arada tutmaya çalışırken; elektrik alanı, bir yük kuvvetiyle damlacıktan dışarıya doğru çekerek bir güç oluşturur.
Beroz: “Bir noktada, eğer elektrik alanı yeterince güçlüyse, damlacık elektrik kuvvetini dengeleyen bir şekil bulamaz ve bu noktada dengesizleşir ve patlar.”
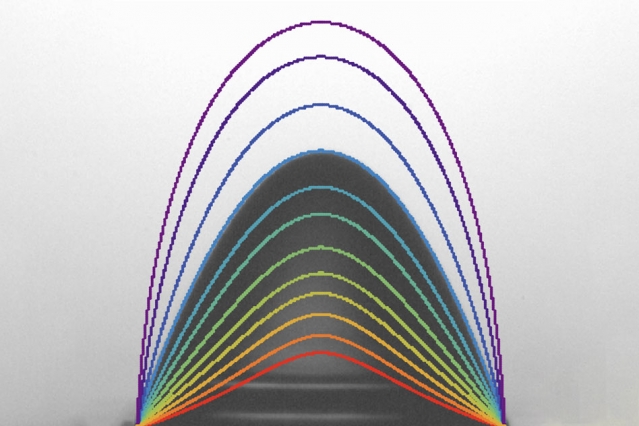
O ve ekibi; patlamadan hemen önce, damlacık kritik derecede stabil bir şekle sokulduğunda, incelemeye başladılar. Ekip; su damlacıklarını, elektrik alanını üretmek için elektrikli bir metal plaka üzerine yavaşça dağıttıkları bir deney yaptılar. Her damlacığın çarpık şekillerini kaydetmek için yüksek hızlı bir kamera kullandılar.
Beroz: “İlk başta deney gerçekten sıkıcı; damlacık şeklinin yavaş yavaş şekil değiştirdiğini ve ardından aniden patladığını izliyorsunuz.”
Beroz; farklı büyüklükteki damlacıklar üzerinde ve çeşitli elektrik alanı kuvvetleri altında deney yaptıktan sonra, video karesini her damlacık patlamasından hemen önce izole etti. Daha sonra kritik olarak stabil şeklini belirledi ve damlacık hacmi, yüksekliği ve yarıçapı gibi birkaç parametre hesapladı. Her damlacıktan gelen verileri çizdi ve şaşkınlıkla, hepsinin açıkça düz bir çizgi boyunca düştüğünü farketti.
Beroz: “Teorik bakış açısından, sorunun matematiksel karmaşıklığı göz önüne alındığında beklenmedik şekilde basit bir sonuçla karşılaştık. Damlacıklar için patlama ölçütünü hesaplamanın göz ardı edilmiş fakat basit bir yolu olabileceğini gördük.”
Yavaş yavaş artan gücü olan bir elektrik alanına maruz kalan bir su damlası; apeksinden ince, elektrikli bir sis yayarak aniden patlar.
Yüksekliğin üzerindeki ses
Fizikçiler; bir elektrik alanındaki sıvı damlacıklarının, birleştirilmiş bir lineer doğrusal olmayan diferansiyel denklem seti ile temsil edilebileceğini uzun zamandır biliyorlardı. Bununla birlikte, bu denklemlerin çözülmesi inanılmaz derecede zordur. Bir çözümü bulmak için; elektrik alanın konfigürasyonunu, damlacık şeklini ve damlacık içindeki basıncın aynı anda belirlenmesi gerekir.
Beroz: “Genelde fizikte durum bu: Yönetim denklemlerini yazmak kolaydır, ancak bunları çözmek gerçekten çok zor. Fakat damlacıklar ve sorunu en baştan tanımlamak için belirli bir fiziksel parametre kombinasyonunu seçerseniz, bir çözümün birkaç satırda elde edilebileceği ortaya çıkıyor. Aksi takdirde imkansızdır.”

Geçmişte bu denklemleri çözmeye çalışan fizikçiler bunu; diğer parametrelerin yanı sıra damlacık yüksekliğini, damlacık şeklini karakterize etmek için kolay ve doğal bir seçenek olarak düşünerek yaptılar. Fakat Beroz farklı bir seçim yaptı; denklemleri damlacıkların yüksekliğinden ziyade hacmine göre yeniden adlandırdı. Bu; problemi çözmesi kolay bir formüle dönüştürmek için kilit fikirdi.
Beroz: “Son 100 yıl boyunca, konvansiyonun yüksekliği seçildi. Fakat bir damlacık deforme olduğunda, yüksekliği değişir ve bu nedenle problemin matematiksel karmaşıklığı yükseklikte doğaldır. Diğer taraftan, elektrik alanı, ne şekilde deforme olursa olsun damlacık hacmi sabit kalır. ”
Beroz; denklemleri yalnızca bir damlacık hacmiyle aynı şekilde “sabit” parametreler kullanarak formüle ederek, “denklemin karmaşık, çözülemeyen kısımları, deney sonuçlarına uyan basit bir denklem bırakarak iptal edildiğini belirtiyor.
Spesifik olarak; ekibin elde ettiği yeni formül beş parametre ile ilgilidir: Bir damlacağın yüzey gerilimi, yarıçapı, hacmi, elektrik alanı kuvveti ve damlacık çevresindeki havanın elektrik geçirgenliği… Bu parametrelerden dördünü formüle eklemek beşinci değeri hesaplar.
Beroz; mühendislerin, ince bir sprey üretmek için elektrikli bir ağızlığın ağzında tutulan bir damlacık patlamasını içeren elektrospreyleme gibi teknikleri geliştirmek için formülü kullanabileceğini söylüyor. Elektrospreyleme; genel olarak bir çözeltiden biyomolekülleri aerosolize etmek için kullanılır. Böylece ayrıntılı analiz için bir spektrometreden geçebilirler. Bu teknik ayrıca uzayda itme ve itme uyduları üretmek için de kullanılır.
Beroz: “Sıvıları ve elektriği içeren bir sistem tasarlıyorsanız, her gün kullanabileceğiniz böyle bir denklem elde etmek çok pratiktir.”